On generating prime numbers quickly in Python

I wanted to generate a long list of prime numbers (all prime numbers below 1B).

The terrible way

I remember watching a terrible python tutorial not so long ago with a terrible (if not the worst) way of doing this:

from tqdm import tqdm

def is_prime(n):
    for i in range(2, n):
        if n % i == 0:
            return False
    return True

def prime(n):
    return [is_prime(i) for i in tqdm(range(1, n+1))]

This is a terrible way of computing all prime number up until \(n\) for several reasons:

• primality tests are less efficient than using sieves when trying to generate a list of primes;
• there is no need to look above \(\sqrt{k}\) when determining if \(k\) is prime. Let’s time it for \(n = 100\ 000\):

  CPU times: user 30.8 s, sys: 12 ms, total: 30.8 s
  Wall time: 30.8 s
  

Sieve of Eratosthenes

This algorithm has been attributed to Eratosthene of Cyrene, a Greek mathematician (see its Wikipedia article) and eliminates the multiples of numbers:

• we generate an array of length \(n\):

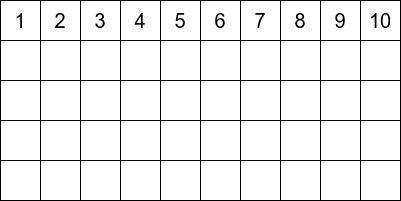
• we ignore the \(1\) and start at \(i=2\) and eliminate all its multiples:

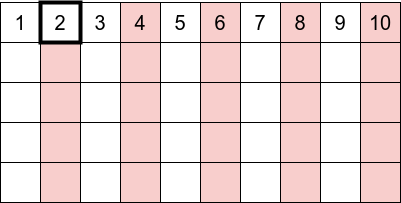
• with \(i=3\), we eliminate all its multiples:

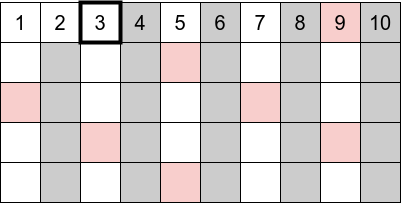
• and so on:

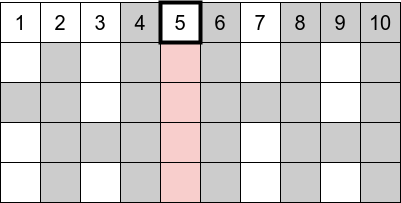
It has a complexity of \(O(N \log{N})\).
A first implementation would be:

from tqdm import tqdm

def eratosthene(n):
    is_prime = [1 for _ in range(n)]
    
    for i in tqdm(range(2, n+1)):
        for j in range(2, n//i + 1):
            is_prime[i*j-1] = 0
    
    is_prime[0] = 0
    return is_prime

If we time it for \(n = 100\ 000\):

CPU times: user 144 ms, sys: 4.06 ms, total: 148 ms
Wall time: 147 ms

Over 200× faster. But we can improve that. Storing such a big array can be troublesome and storing the numbers is a waste of memory. We can settle with only storing a \({0, 1}\) array is_prime. For efficiency purpose, we will use a numpy array of numpy.bool. Numpy smallest variable size is bool, which uses 1 byte of memory. Also, if is_prime[i] == 0, there’s no need to change its multiples indices entries as they must have already been set to 0 (if there are two integers \(k, p\) such that \(i=k \times p\), then all of its multiples are also multiples of \(k\) and \(p\) and must have already been flagged as non prime). We can further leverage numpy’s array operations to change all the multiple’s indices in the is_prime array (is_prime[2*i-1::i]), and avoid the inner loop. Finally, we can lower the loop’s upper bound to \(\frac{n}{2} + 1\) as is_prime[2*i-1::i] == array([]) for \(i > \frac{n}{2}\):

from tqdm import tqdm
import numpy as np

def eratosthene(n):
    is_prime = np.ones((n), dtype=np.bool)
    
    for i in tqdm(range(2, (n//2)+1)):
        if not is_prime[i]:
            continue
        is_prime[2*i-1::i] = 0
    
    is_prime[0] = 0
    return is_prime

Let’s time it for \(n = 100\ 000\):

CPU times: user 46.3 ms, sys: 0 ns, total: 46.3 ms
Wall time: 45.3 ms

But storing each flag in an 8 bits variable is a waste of memory… We can improve that. The Python library bitarray allows to use arrays of 1 bit elements. This further improves the memory savings and the speed of our implementation:

from tqdm import tqdm
from bitarray import bitarray

def eratosthene(n):
    is_prime = bitarray(n)
    is_prime.setall(1)
    
    for i in tqdm(range(2, (n//2)+1)):
        if not is_prime[i]:
            continue
        is_prime[2*i-1::i] = 0
    
    is_prime[0] = 0
    return is_prime

Let’s time it for \(n = 100\ 000\):

CPU times: user 18.5 ms, sys: 0 ns, total: 18.5 ms
Wall time: 18.4 ms

Which leads to a final \(1673\times\) speed-up with an optimized memory footprint (\(\frac{1}{8}\times\) improvement).

Sieve of Atkin

The sieve of Atkin is an even more sophisticated algorithm created in 2003 relying on modulo 60 remainders and bit flipping. The complete algorithm is described on its Wikipedia article. It has a linear complexity (\(O(N)\)) or sublinear depending on the version of the algorithm (\(O(\frac{N}{\log{N}})\)) Inspired by this implementation of the sieve and using as many as the previous tricks, we time its execution for \(n = 100\ 000\).

However, when timing it:

CPU times: user 149 ms, sys: 0 ns, total: 149 ms
Wall time: 148 ms

Even though the Sieve of Atkin has a better time complexity, it doesn’t mean that it has a faster implementation, it only gives you asymptotical information. The iterative nature of this algorithm prevents from using tricks to speed up the process as we did the the sieve of Eratosthene.

Conclusion

>>> is_prime = eratosthene(1_000_000_000)
100%|████████████████████| 499999999/499999999 [04:41<00:00, 1773674.29it/s]

In under 5 minutes, we obtained the list of all prime numbers below 1 billion using the sieve of Eratosthene.